Calcolo della Varianza in Excel: Una Guida con Esempi
La varianza è una misura statistica che ci dice quanto un insieme di numeri è distribuito. È un concetto fondamentale in finanza, scienza e molti altri campi, aiutandoci a comprendere la variabilità o la dispersione all'interno dei nostri set di dati. Excel offre un modo semplice per calcolare la varianza, rendendola accessibile sia per principianti che per utenti avanzati. In questo articolo, esploreremo come farlo con esempi chiari.
Cos'è la varianza?
Introduzione alle funzioni di varianza in Excel
Come calcolare la varianza in Excel?
- VAR.S vs VAR.P – Calcolo della varianza da un campione o da una popolazione
- VAR.S vs VARA – Calcolo della varianza includendo o escludendo testi e valori logici
Varianza vs Deviazione standard
Cos'è la varianza?
La varianza è un termine statistico che descrive l'entità con cui i numeri in un insieme di dati differiscono dalla media, o valore medio, dei numeri. Essenzialmente, misura quanto sono dispersi i numeri. Un punto chiave per comprendere la varianza è riconoscere che quantifica il grado di variazione o dispersione all'interno di un insieme di valori. Una varianza alta indica che i numeri sono ampiamente distribuiti; una varianza bassa suggerisce che sono raggruppati vicino alla media.
Un semplice esempio per illustrare la varianza:
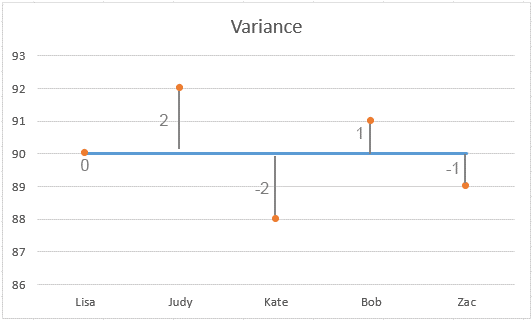
Scenario: Consideriamo una classe con cinque studenti e i loro punteggi in un test di matematica su 100. I punteggi sono 90, 92, 88, 91 e 89.
Calcola la Media: Prima troviamo il punteggio medio (media). La media è
Calcola la Varianza: Poi, calcoliamo la varianza. Questo comporta sottrarre la media da ogni punteggio, elevare al quadrato il risultato e poi fare la media di queste differenze al quadrato.
= [0 + 4 + 4 + 1 + 1] / 5
= 10 / 5
= 2
Un grafico mostrava la distribuzione dei punteggi:
Comprendere il risultato:
Bassa Varianza: In questo esempio, la varianza è 2. Questo è relativamente basso, indicando che la maggior parte dei punteggi è vicina alla media (90). Minore è la varianza, più i singoli numeri nell'insieme sono vicini alla media.
Varianza Zero: Se tutti gli studenti avessero ottenuto esattamente 90, la varianza sarebbe stata 0, indicando nessuna variabilità. Ogni punteggio sarebbe stato lo stesso.
Alta Varianza: Al contrario, una varianza più alta indicherebbe che i punteggi sono più dispersi rispetto alla media, mostrando una maggiore variabilità nelle prestazioni degli studenti.
In sintesi, la varianza ci fornisce un valore numerico che aiuta a quantificare quanto i punteggi (o qualsiasi insieme di numeri) si discostano dal valore medio, fornendo informazioni sulla consistenza o variabilità dei dati.
Introduzione alle funzioni di varianza in Excel
Excel fornisce diverse funzioni per calcolare la varianza, ciascuna progettata per diversi scenari di dati.
Comprendere queste funzioni è cruciale per un'analisi statistica accurata
VAR.S (Varianza del Campione, solo numeri):
- Calcola la varianza basata su un campione della popolazione.
- Miglior utilizzo quando si analizza un sottoinsieme di dati per inferire sull'intero.
VAR.P (Varianza della Popolazione, solo numeri):
- Calcola la varianza per l'intera popolazione.
- Ideale quando si dispone di dati completi e non solo di un campione.
VARA (Varianza del Campione, inclusi testi e valori logici):
- Simile a VAR.S ma include testi e valori logici nel calcolo (il testo è trattato come 0, VERO come 1, FALSO come 0).
- Utile quando il tuo set di dati contiene tipi misti (numeri, testi e valori logici).
VARPA (Varianza della Popolazione, inclusi testi e valori logici):
- La versione della varianza della popolazione di VARA.
- Include tutti i tipi di dati nel calcolo della varianza per l'intera popolazione.
VAR (Varianza del Campione Legacy):
- Una versione precedente di VAR.S, principalmente usata in Excel 2007 e versioni precedenti.
- Si consiglia di usare VAR.S nelle versioni più recenti per coerenza e chiarezza.
VARP (Varianza della Popolazione Legacy):
- La versione precedente di VAR.P.
- Come VAR, si consiglia di usare VAR.P nelle versioni più recenti di Excel.
Differenze e Confronti:
- Campionamento vs. Popolazione: VAR.S e VARA sono per campioni, mentre VAR.P e VARPA sono per l'intera popolazione.
- Considerazione sul Tipo di Dati: VARA e VARPA includono testi e valori logici nel calcolo, a differenza di VAR.S e VAR.P.
- Funzioni Legacy vs. Moderne: VAR e VARP sono funzioni più vecchie e possono essere sostituite da VAR.S e VAR.P per una migliore compatibilità con le versioni attuali di Excel.
Tabella di confronto:
| Funzione | Tipo di Dati Considerati | Popolazione o Campione | Caso d'uso |
| VAR.S | Solo Numeri | Campione | Varianza del campione per dati numerici |
| VAR.P | Solo Numeri | Popolazione | Varianza della popolazione per numeri |
| VARA | Numeri, Testi, Logici | Campione | Varianza del campione per dati misti |
| VARPA | Numeri, Testi, Logici | Popolazione | Varianza della popolazione per dati misti |
| VAR | Solo Numeri | Campione | Funzione legacy per la varianza del campione |
| VARP | Solo Numeri | Popolazione | Funzione legacy per la varianza della popolazione |

Sblocca la Magia di Excel con Kutools AI
- Esecuzione Intelligente: Esegui operazioni sulle celle, analizza i dati e crea grafici — tutto guidato da semplici comandi.
- Formule Personalizzate: Genera formule su misura per ottimizzare i tuoi flussi di lavoro.
- Codifica VBA: Scrivi e implementa codice VBA senza sforzo.
- Interpretazione delle Formule: Comprendi facilmente formule complesse.
- Traduzione del Testo: Superare le barriere linguistiche all'interno dei tuoi fogli di calcolo.
Come calcolare la varianza in Excel?
In questa sezione, forniremo due esempi per dimostrare come calcolare la varianza in Excel e spiegheremo le differenze tra le varie funzioni di varianza. Di conseguenza, vedrai che diverse funzioni di varianza producono risultati completamente diversi per gli stessi dati di esempio.
VAR.S vs VAR.P – Calcolo della varianza da un campione o da una popolazione
Scenario: Calcolo della varianza per un piccolo campione di una popolazione rispetto all'intera popolazione.
Esempio: Calcola la varianza per i valori nella colonna A2:A12.
Formula: Seleziona una cella vuota e digita una delle seguenti formule secondo necessità, quindi premi il tasto Invio.
Ottenere le varianze per il campione di un grande set di dati (supponendo che i valori in A2:A12 siano parti di un grande set di dati)
=VAR.S(A2:A12)
Ottenere la varianza per l'intera popolazione (supponendo che i valori in A2:A12 siano l'intero set di dati)
=VAR.P(A2:A12)
Come vedi, gli stessi valori ma usando diverse funzioni di varianza daranno risultati diversi.
Perché i risultati di VAR.S e VAR.P sono diversi?
- VAR.S: Questa funzione viene utilizzata quando il tuo set di dati rappresenta un campione di una popolazione più ampia. Calcola la varianza basata sul metodo "n-1", dove "n" è il numero di punti dati nel campione. L'uso di "n-1" invece di "n" come denominatore corregge il bias nel campione, rendendolo uno stimatore imparziale della varianza della popolazione. Fornisce una stima di come i dati nel campione variano intorno alla media del campione.
- VAR.P: Questa funzione viene utilizzata quando il tuo set di dati rappresenta un'intera popolazione, non solo un campione di essa. Calcola la varianza basata sul metodo "n", dove "n" è il numero di punti dati nella popolazione. Presuppone che il set di dati copra l'intera popolazione, quindi non c'è bisogno di correggere il bias come in VAR.S.
- In sintesi, la differenza chiave è nel denominatore della formula. VAR.S usa "n-1" per tenere conto della natura campionaria dei dati, mentre VAR.P usa "n" per i dati della popolazione dove non c'è campionamento coinvolto. A seconda del tuo set di dati e se si tratta di un campione o di una popolazione completa, dovresti scegliere la funzione appropriata per calcolare la varianza.
VAR.S vs VARA – Calcolo della varianza includendo o escludendo testi e valori logici
Scenario: Decidere se includere valori logici e testi nel calcolo della varianza.
Esempio: Calcola la varianza per i valori nella colonna A2:A12.
Formula: Seleziona una cella vuota e digita una delle seguenti formule secondo necessità, quindi premi il tasto Invio.
Ottenere le varianze per il campione di un grande set di dati ignorando testi e valori logici.
=VAR.S(A2:A12)
Ottenere la varianza per il campione di un grande set di dati includendo testi e valori logici.
=VARA(A2:A12)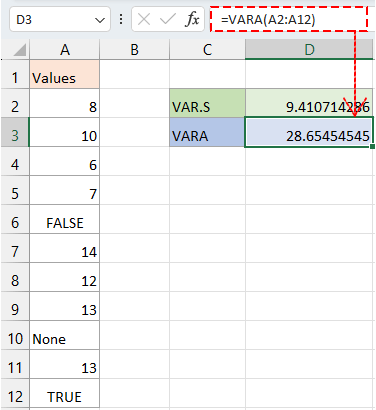
Rendi i calcoli di data e ora rapidi
Kutools per Excel's Date Time Helper è uno strumento incredibilmente efficiente progettato per semplificare calcoli complessi di data e ora. Provalo e scopri come trasforma la tua esperienza di gestione dei dati!
Varianza vs Deviazione standard
Somiglianze:
Misura di Dispersione:
Sia la varianza che la deviazione standard sono misure statistiche utilizzate per descrivere la dispersione o la diffusione all'interno di un insieme di dati. Quantificano quanto i singoli numeri nell'insieme si discostano dalla media (valore medio).
Analisi dei Dati:
Entrambe sono comunemente utilizzate nell'analisi statistica per comprendere la variabilità dei dati. Sono essenziali in settori come la finanza, la ricerca, il controllo qualità e altro ancora.
Calcolato dalla Media:
Il calcolo sia della varianza che della deviazione standard inizia con la media dell'insieme di dati. Valutano la variabilità in relazione a questo valore centrale.
Differenze:
Unità di Misura:
Varianza: Unità quadrate dei dati originali. Ad esempio, se i dati sono in metri, la varianza sarà in metri quadrati.
Deviazione Standard: Stesse unità dei dati originali. Continuando l'esempio, se i dati sono in metri, la deviazione standard sarà anch'essa in metri.
Interpretazione:
Varianza: Fornisce una stima al quadrato che può essere meno intuitiva da interpretare perché non è nella stessa scala dei dati originali.
Deviazione Standard: Più interpretabile poiché è nelle stesse unità dei dati. Indica la distanza media dei punti dati dalla media.
Definizione Matematica:
Varianza: La media delle differenze al quadrato dalla Media.
Deviazione Standard: La radice quadrata della varianza.
Sensibilità ai Valori Estremi:
Varianza: Più sensibile agli outlier perché eleva al quadrato le differenze.
Deviazione Standard: Anche se influenzata dagli outlier, è meno sensibile rispetto alla varianza a causa della radice quadrata.
Applicazioni:
Varianza:
Utilizzata quando l'attenzione è sulla grandezza al quadrato della dispersione.
Benefica nei modelli statistici e nei calcoli dove è necessario elevare al quadrato per annullare i valori negativi.
Spesso utilizzata nei modelli finanziari per la valutazione del rischio, poiché misura la volatilità.
Deviazione Standard:
Più comunemente utilizzata nei rapporti e nelle applicazioni quotidiane grazie alla sua relazione diretta con la scala dei dati.
Essenziale nella ricerca empirica per comprendere la variabilità.
Frequentemente utilizzata nel controllo qualità, nei bollettini meteorologici e nei punteggi standard nei test.
Conclusione:
Sebbene la varianza e la deviazione standard servano entrambe a misurare la dispersione di un insieme di dati, le loro applicazioni differiscono a causa della loro unità di misura e interpretazione. La deviazione standard, con la sua relazione diretta alla scala dei dati, tende ad essere più user-friendly, soprattutto in contesti pratici ed everyday. La varianza, d'altra parte, è spesso più adatta a modelli matematici e statistici.
Questa panoramica e confronto dovrebbero fornire una chiara comprensione di quando e perché utilizzare ciascuna funzione di varianza in Excel, consentendo analisi dei dati più accurate e significative. Per ulteriori strategie rivoluzionarie di Excel che possono migliorare la gestione dei tuoi dati, esplora ulteriormente qui.
Gli strumenti per la produttività di Office migliori
Kutools per Excel - Ti aiuta a distinguerti dalla massa
Kutools per Excel vanta oltre 300 funzionalità, garantendo che ciò di cui hai bisogno sia a portata di clic...
Office Tab - Abilita la lettura e la modifica a schede in Microsoft Office (incluso Excel)
- Un secondo per passare tra decine di documenti aperti!
- Riduce centinaia di clic del mouse ogni giorno, dì addio alla mano del mouse.
- Aumenta la tua produttività del 50% quando visualizzi e modifichi più documenti.
- Porta Schede Efficienti a Office (incluso Excel), proprio come Chrome, Edge e Firefox.
Indice
- Cos'è la varianza?
- Introduzione alle funzioni di varianza in Excel
- Come calcolare la varianza in Excel?
- VAR.S vs VAR.P – Calcolo della varianza da un campione o da una popolazione
- VAR.S vs VARA – Calcolo della varianza includendo o escludendo testi e valori logici
- Varianza vs Deviazione standard
- Articoli Correlati
- Migliori Strumenti di Produttività per Office
- Commenti